Transformation of a Logarithmic Function
While we’re on the topic of logarithms, lets do a little bit of review.
This article is dedicated to the kids in my neighbourhood. You are the future. What will your contribution be to the generation that follows you? I know that you can imagine a better world for everyone, just like the people I’m writing about. Keep practising your ScienceTechEngineeringMath skills! Trust me, if you don’t then they get rusty !
Having said that, I know we didn’t get around to discussing logarithms but we did learn about exponents (whether your realize it or not ;). REMEMBER: an exponent represents multiplying a number by itself.
SQUARE FUNCTION
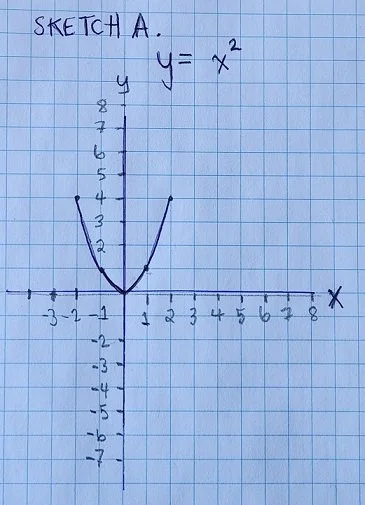
For example, here’s a sketch of the values for a square function. That’s a function where a number is multiplied by itself. (See Sketch A. BTW, I apologize for these hand-drawn graphs. Incidentally, I tried to compress these images so they wouldn’t take too long to load on your computer screen.)
Sketch A., where y = x-squared
In Sketch A. the function we’re graphing can be expressed as x-squared, where x represents the number we’re multiplying: x(x) equals x-squared. In this graph, the y-value represents the result of our exponential function. We can see that the value of y is always positive. That’s why it’s smiling! This is because it doesn’t matter what number x represents, if you square a number the result will always be positive (or greater than zero). On a graph, the square function is shaped like a U.
ABSOLUTE-VALUE FUNCTION
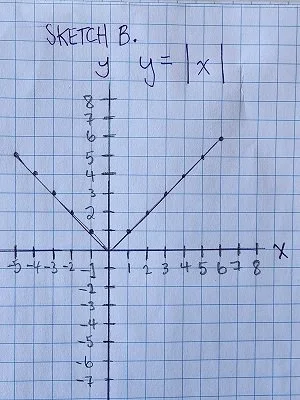
There are other functions that have a similar range of y values. For example, the absolute-value function always returns a positive y-value (see Sketch B.).
Sketch B. where y equals the absolute value of x.
When you sketch the absolute-value function as a graph it’s shaped like a V. This function measures the distance of x from zero, and can be expressed as: y = |x|
Again, x is the input value of the function and y is the output value.
LOGARITHMIC FUNCTION
You’re probably wondering what all of this has to do with a logarithm.
Well, a logarithmic function returns the exponent to which a base is raised given a particular input. In other words, how many times must a base be multiplied by itself to return the x-value? The graph of a logarithmic function generally has the shape of a stretched, tipped-over U (see Sketch C.).
Sketch C., where y = log x with a base of 2
In my graph, I’m using a base of 2. This means all the values represented are related to the number of times 2 is multiplied by itself. Our input is the x-value that we feed into the logarithm. The output is an exponent. We represent that exponent as a y-value, where y = log x with a base of 2.
You might think that this logarithmic function resembles our square function in Sketch A. Be careful not to confuse a base number with its exponent.
In the square(exponential) function the base number is variable and the exponent is constant.
In a logarithmic function the base remains constant while our input for the x-value determines the value of y (the exponent). I happen to be using base 2 to illustrate the logarithmic function, but that’s because it’s easier for me to think in base 2 ;)
ABSOLUTE-VALUE FUNCTION TRANSFORMS THE LOGARITHM
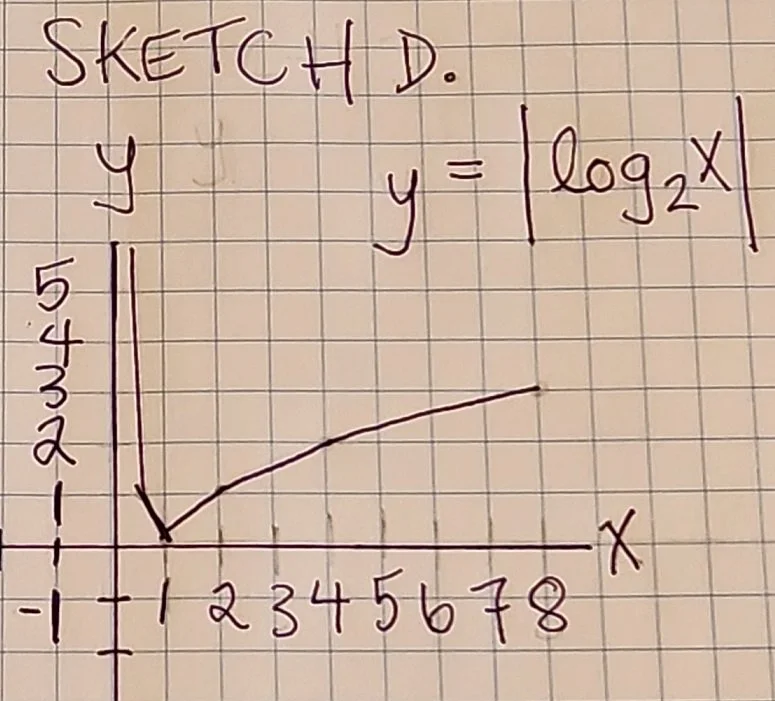
OK so we know a little about elementary logarithmic functions now, what happens when we combine them with another function … maybe our old friend the absolute-value function? (See Sketch D.)
Sketch D., y = |log x| with base 2
In this graph, we’re witnessing the effect of our absolute value function on a logarithm. It’s been transformed! Now the y-value is always positive regardless of the x-value. It’s important to remember that once we apply the absolute value function to the result of a logarithm, y no longer represents an exponent for our base. Our y-value represents an exponent’s distance from zero, or its absolute value. This transformation can be expressed as:
y = |log x|
Hey now that you know how to transform a logarithmic function using absolute value, you can imagine (or graph) other types of transformation… Here’s a couple suggestions:
y = - log x
y = log |x|
In conclusion if you’re able to transform a logarithmic function, imagine all the other functions you can transform when you set your mind to it :)